本サイトは、データと統計学を利用して競馬をより楽しむことを目的とするサイトです。予想ではなくデータの提供を通じて、皆さんのより良い競馬ライフの一助になれば幸いです。
データの提供は、棒グラフなどを用いた視覚的かつ簡単な解説でわかりやすい提供します。
棒グラフとは、縦軸にデータ量をとり、棒の高さでデータの大小を表したグラフです。(縦横が逆の場合もあります。)
値の高い項目や低い項目を判別するのに有効なグラフで、データの大小が、棒の高低で表されるので、データの大小を比較するのに適しています。(統計局HPより抜粋)
本サイトでも棒グラフを使用してデータをまとめ、皆さんに提示していきます。しかし、棒グラフは単純な構造ゆえに、正しい情報をうまく伝えることができないことがあります。このページでは、皆さんにお見せするグラフがどのようにしてできているのかを解説します。
本ページを最後まで読むことで、本サイトが提供するグラフについてより理解を深めることができ、結果的により良い予想へつなげることができます。
使用するグラフの紹介
下に、過去23回分の京成杯について、馬番と3位以上の関係性に着目してデータをまとめたグラフを用意しました。
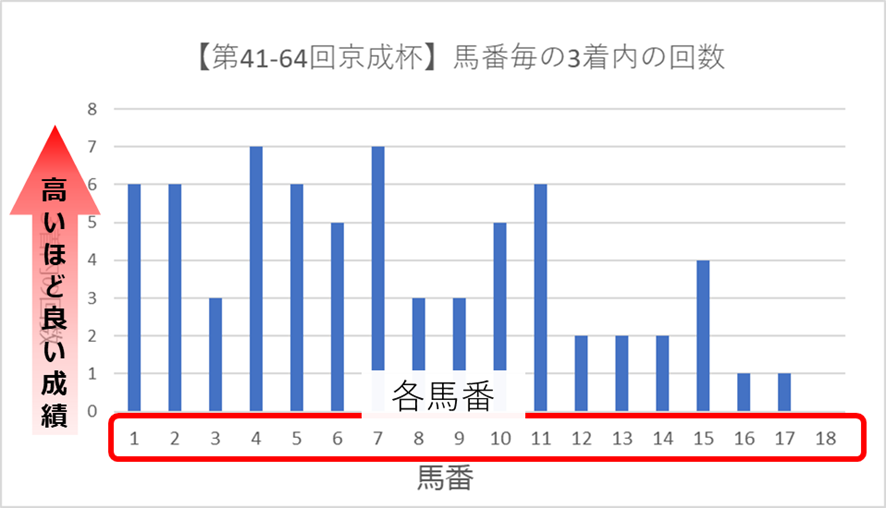
縦軸が3位以上の回数。横軸に各馬番が記載されています。
棒の高さが高いほど、3着内に入った回数が多くなり、成績が良いということになります。
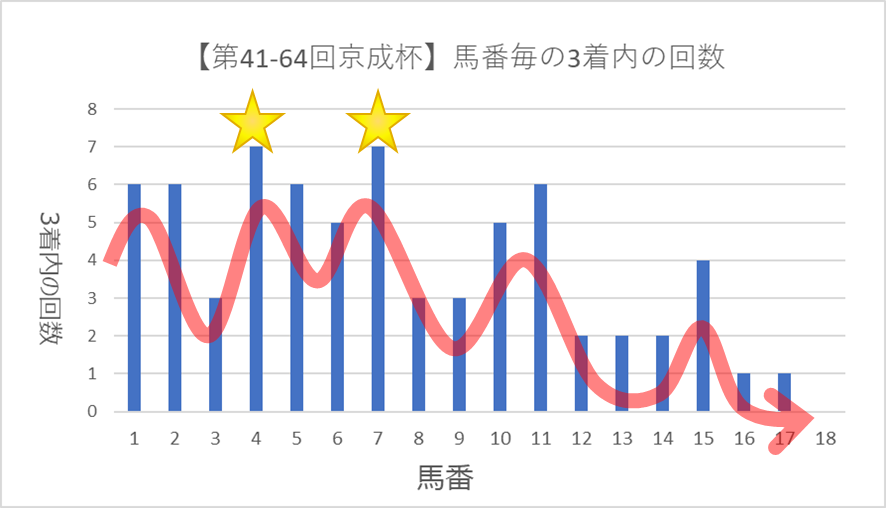
各馬番毎の棒グラフの高さを比較すると、デコボコしていて馬番毎の成績に違いがありそうだということがわかります。
4番と7番が7回を記録しており、最も良い成績を残しているということが読み取れます。
では、1番が記録してる6回や6番の5回という成績は、良いのでしょうか?
また、棒グラフが低いと成績が悪いということはわかりますが、どこから成績が悪いといえるのでしょうか?
この問題を解消するために本サイトでは、平均値(期待値)を目安として使用しています。
例えば今回の条件だと、過去23回で3位以上に入った馬は69頭です。
23×3 = 69
どの馬番でも3位以上になる確率(なりやすさ)が変わらない場合、69頭は18の馬番に均等に分かれます。下記のように計算すると、各馬番に3位以上に入る馬が約4頭ずつ入ることになります。これが目安となる平均値となります。
69/18 = 3.833・・・
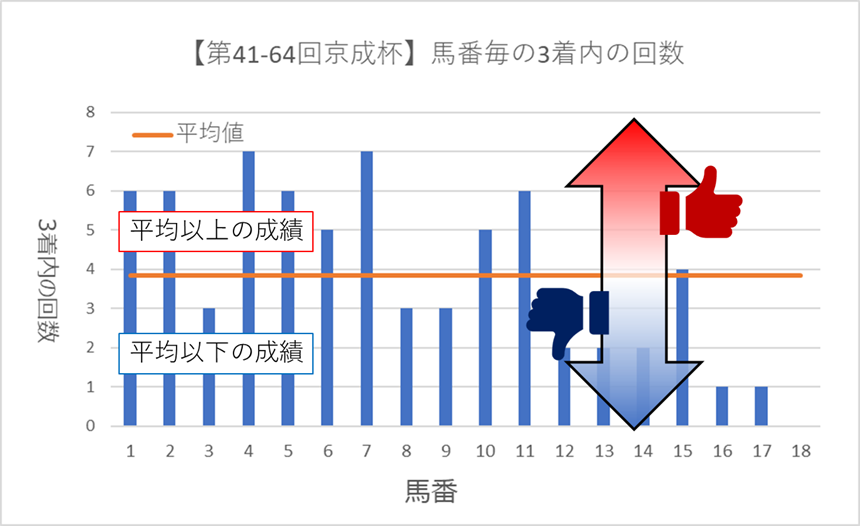
これで平均値を基準として、成績が良い馬番と成績が悪い馬番を判別できるようになりました。
本当の平均値(期待値)
上記で算出し、基準として利用することにした4頭という平均値(期待値)。しかし、本当に正しい値なのでしょうか。
残念ながら、今回は正確な値ではありません。ポイントとなるのは、18という馬番です。
下に、過去23回分の京成杯に出走した各馬番の頭数をまとめたグラフを提示します。
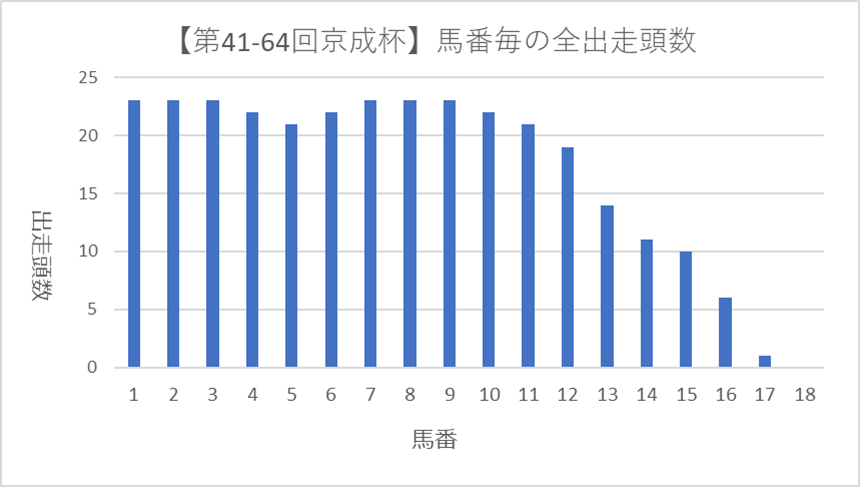
18頭で出走したことは一度もなく、基本的に12頭程度で開催されていることがわかります。
※日本の競馬は2~18頭で走ることができる(競馬法施行規則参照)。
つまり、より正確な平均値(期待値)を求めるためには、69頭を12前後の数字で割る必要があります。
この[12前後]の数字をより具体化するために、今回も平均を利用して算出していきます。
計算内容は以下の通りです。
過去23回分の記録で、最後まで走り切った頭数の合計値を求める(京成杯:307頭)。次に、全頭数を集計したレース回数で割ることで、1レース当たりの平均出走頭数を得ることができます(京成杯:13.3頭/レース)
以上のことから、馬番毎の平均3着内回数の算出には、13.3を利用することがより正確であると考えられます。
実際に下記の通り計算してみると5.2となり、過去23回のレース結果をまとめると1つの馬番あたり約5頭3着内の馬がいるという結果になりました。
69頭/13.3番 ≒ 5.2 頭/馬番
この値は、前段で算出した値と異なる結果となりました。
4頭と5頭は、わずか1頭の差ではありますが、最大値が7頭である本グラフでは、大きな差になり得ます。細かい点ではありますが、前提条件や出走環境を正しくグラフへ反映させることが大切です。
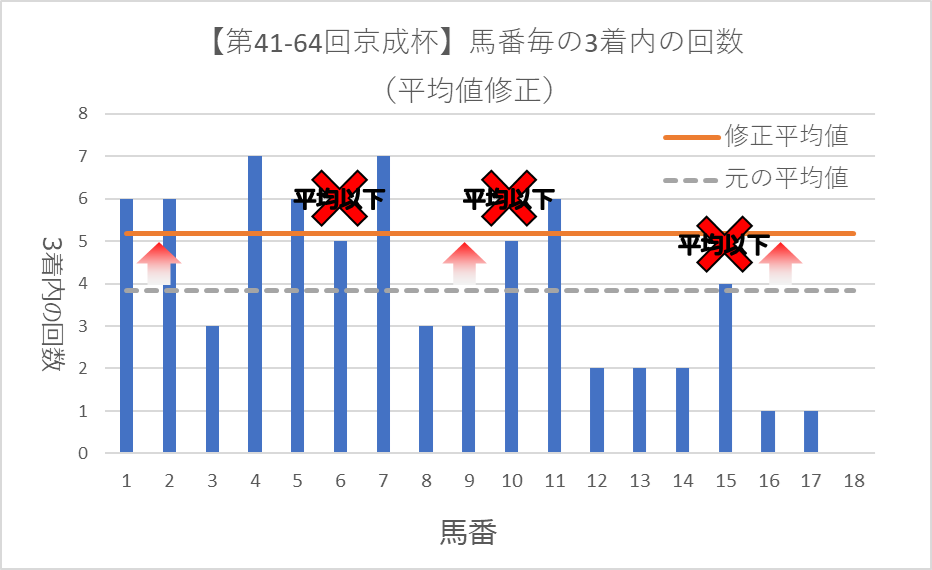
平均値(期待値)との差
1レース当たりの出走頭数の平均を用いることで、より正確な平均値(期待値)を求めることができました。
さて、このグラフを用いて、正しく馬番毎の成績を理解することができるでしょうか?
残念ながらこちらもまた、正しく理解しきれているとは言えません。
今回のポイントは出走頭数です。
【本当の平均値】でお見せした、各馬番の出走頭数をまとめたグラフを再度掲載いたします。
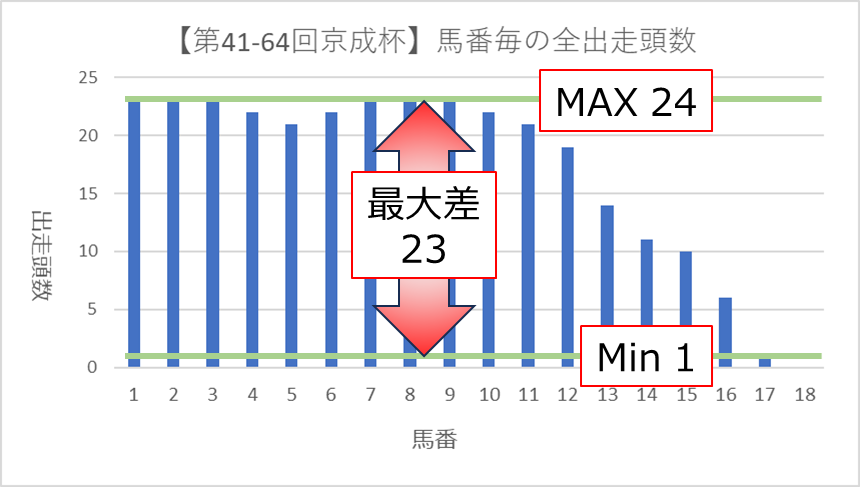
馬番毎に出走頭数が異なり、最大23頭から最小1頭(0頭は除く)まで様々な値をとっています。
前回基準とした数値は5でしたが、この値は過去23回分の3位以上の出走頭数を平均化したものになります。つまり、23回出走した結果、最終的な3位以上の回数が5回になるということです。
今回のレースのように、そもそもの出走回数が異なる場合、出走回数が23回に近いものほど3位以上の回数が5に近づきやすいはずです。また、出走回数が低ければ低いほど3位以上に入る回数は少なくなります。
ここで、3位以上に入った出走頭数のグラフとすべての出走頭数のグラフを一緒に見てみましょう。
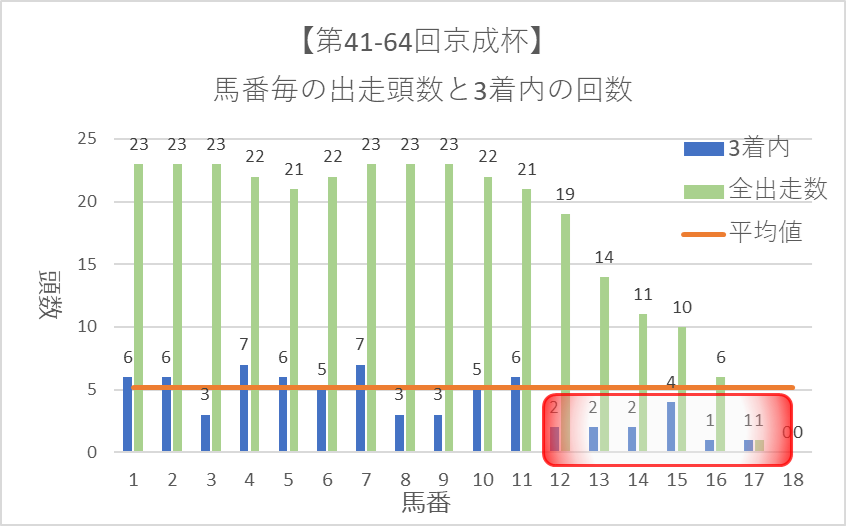
平均出馬数である13以降の馬番では、どの馬番でも基準としてる5回を超えることはできませんでした。
これらの馬番の成績が本当に悪いのではなく、出馬数が少ないために3位以上の数が少ない結果となっています。出走数が少ない馬番を正しく比較するためには、出走数に応じて基準の値を変える必要があります。
出走数に応じた基準値の決定
出走数に応じた基準値の決定には、基準値を使用します。おさらいになりますが、基準値5の意味は、一つの馬番毎に23回出走した場合、5回(頭)3着内に入るということです。
今回のポイントは出走回数です。馬番毎に出走回数がことなるため、基準値もあわせて変化させる必要があります。基準値の関係(23回出走すると5回3着内)を利用して、出走回数に応じた基準値の決定は以下の通り計算できます。
基準値x = 出走回数n × 5 / 23
上記の計算を、すべての馬番で行い、グラフに反映したものが下に示すグラフになります。
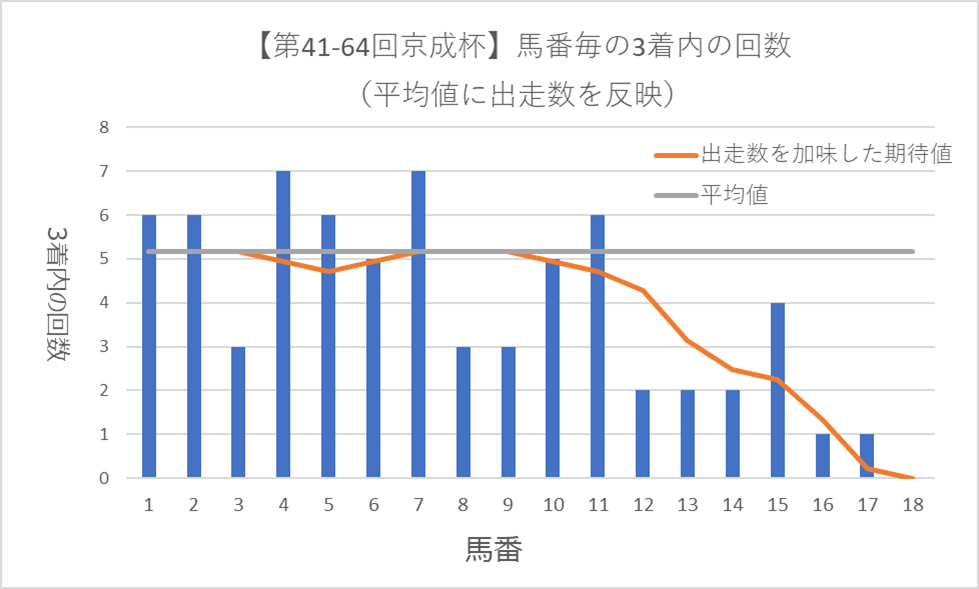
※出走数を考慮すると平均値ではないため期待値として表記しています。
これで、出走回数による基準値の違いも反映したグラフを作成することができ、各馬番毎の成績を確認することができました。
15番や17番といった馬番が期待値以上の成績を残していることがわかるようになり、ただの平均値との比較ではわからなかった、出走数が少ない馬番についても正しく評価することができるようになりました。
割合でのグラフ化
出走数の違いを加味した馬番毎の基準値を作成し、各馬番の成績を確認できるようになりました。しかし、基準値はまちまちであり、馬番同士の成績を比較することが難しくなっています。この問題は、割合を利用するこで解決することができます。
過去23回のレースで3着内の馬は69頭です。また、出走した馬は合計307頭となっています。この2つの値を利用して、出走数に対する3着内の割合を下記の式から約0.225と求めることができます。
69 / 307 ≒ 0.225
3着内の割合(3着内頭数 / 出走頭数)においては、0.225という基準割合はどの馬番でも一定です。
これは【出走数に応じた基準値の決定】で計算した出走回数に応じた基準値の求め方からも読み取ることができます。
基準値x = 出走回数n × 5 / 23
x / n = 5/23
x / n ≒ 0.225
全ての馬番の3位以上の割合と基準割を記載したのが下のグラフになります。なお、見やすいように % で表示しています。
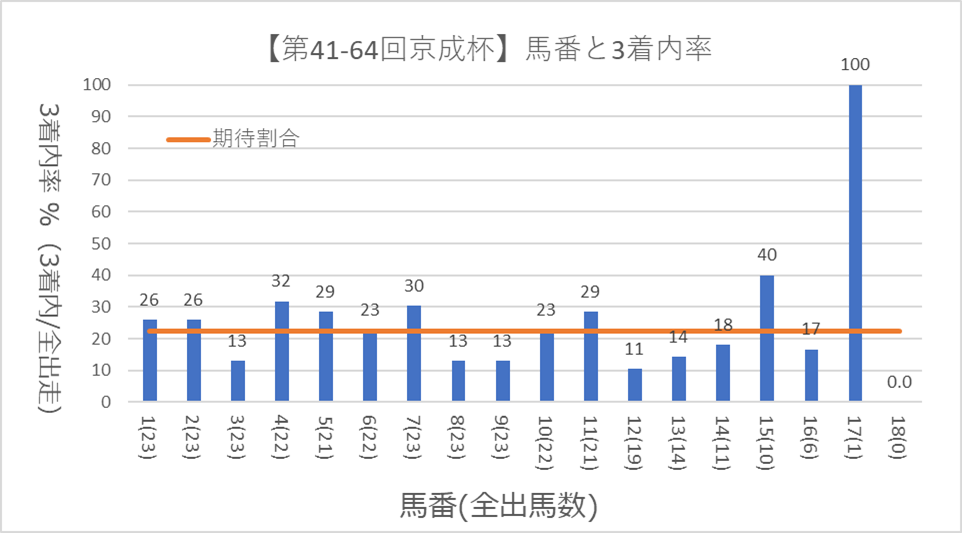
全ての馬番で同じ割合を基準として利用することで、素直にグラフの高さを比較することができるようになりました。
信頼度について
出走数や基準値の違い、馬番毎の比較し易さなどをクリアしたグラフですが、とても大きな問題点があります。
それは、信頼度です。
信頼度と言われてもピンとくる方は少ないと思いますので、具体的な例を出します。
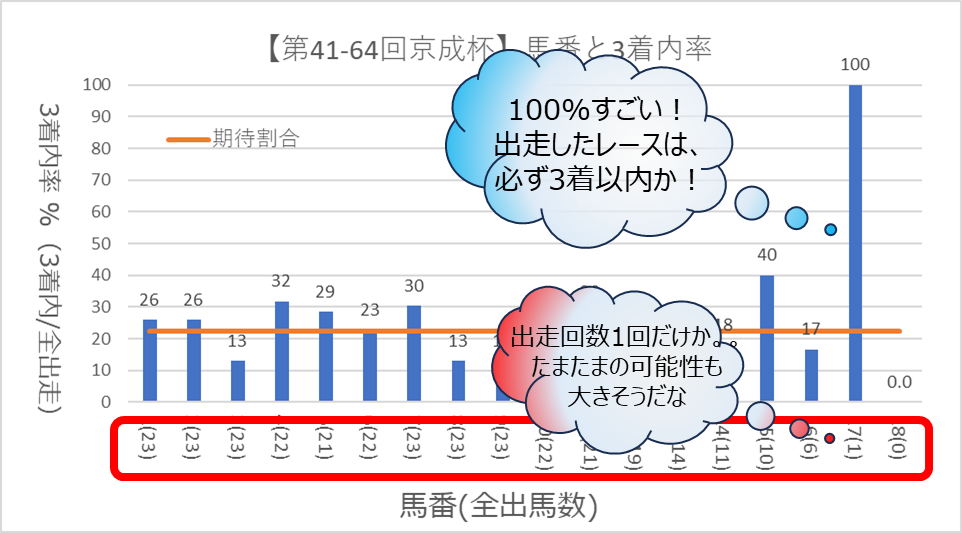
1回出走して1回3着内になった馬番と、1000回出走して900回3位内になっている馬番。割合で考えると、前者が100%、後者が90%となり、前者の方が高くなります。しかし、どちらかの複勝に賭けるのであれば、後者に賭けたくなる方が多いのではないでしょうか。(もちろんオッズや血統など他の要素がない場合に限りますが)
つまり、本サイト内での信頼度※とは、過去のデータ通りになると期待される度合いです。
信頼度を高くするためには、同一条件下でデータ量を増やす必要があります。しかし、競馬において同一条件のデータ量を増やすことは不可能です。本サイトでは、レースでグループ化することで、コース内容などの条件を均一化し、馬の個体差を無視することでデータ量を増やしています。それでも、今回例示してきた馬番などでは、番手によっては十分な信頼度があるとは言い難い状況です。
データ量がわからないと、グラフの信頼度を判断することはできません。本サイトでは、全出走頭数を提示することで、信頼度の判断に活用してもらおう考えています。全出走頭数は、グラフのX軸項目の末尾にカッコ付きで記載しています。グラフを見る際はご注意ください。
※わかりやすい言葉として信頼度を選びましたが、統計学における信頼度とは意味合いが少し異なるので注意してください。
勝率、連帯率、3着内
ここまで利用してきたグラフは、標準的な棒グラフです。本ページ冒頭で示した通り、とてもシンプルで見やすいというメリットがある一方、シンプルゆえに情報が少ないというデメリットがあります。たとえば【割合でのグラフ化】で提示したグラフだと、縦軸が3着内率であるため、実際に活用する方法としては複勝狙いか消し馬の選定のみに限定されます。
少し話がそれますが、JRA公式でもデータ分析情報の開示が行われています。(レース毎にデータ分析の項目があります。是非ご覧ください:JRA サイト今週のレース)そこでは、勝率(1着)、連帯率(2着内)、3着内率に着目して分析が行われています。JRA公式でも提示されてるこれらの情報は、皆様の予想に少なからず役に立つと思います。
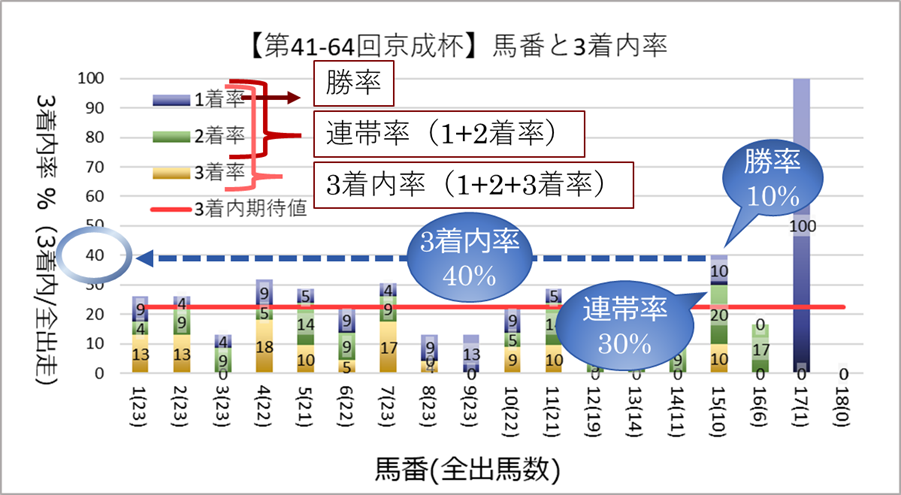
本サイトでは、1着率、2着率、3着率をそれぞれ色分けした積み上げ棒グラフを利用します。具体的な数値もグラフ内で表示しますので、1着率、1+2着率、グラフ縦軸を参照することで、勝率、連帯率、3着内率の情報を得ることができます。見やすさは若干悪くなりますが、それ以上に得られる情報量が増えますので是非ご活用ください。
最後に
競馬は賭け事です。不確定要素を含めて、ご自分の判断かつ無理のない範囲で予想をしていただければと思います。その際、本サイトでまとめられているデータが、皆様の考察と楽しい競馬ライフに貢献できたのであれば、とても嬉しいです。
ここまでお読みいただきありがとうございました!
よろしければ今週のレースデータも見ていってください!
X(旧ツイッター)もやっています。データについて投稿していますので、サイトを見る時間が取れない方は、フォローしてください。

